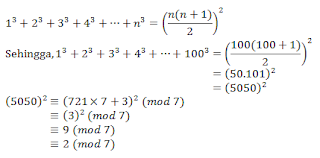Aplikasi Geogebra

Download Here : Geogebra app

Read more...

Pembahasan KSN-K Informatika 2020 No. 16

Soal 16

Perhatikan operasi logika berikut?

((A or not C) and (A and D or A and not D) or A and not C or not C) and (not E and (E or  not B) or (not B or E and E) and(E or B))

Agar pernyataan di atas bernilai true maka nilai A, B, C, D, E harus:

a. A = True, B = True, C = True, D = True, E = False.

b. A = True, B = False, C = False, D = False, E = True.

c. A = True, B = True, C = False, D = True, E = False.

d. A = False, B = True, C = True, D = False, E = False.

e. Jawaban a, b, c, dan d salah

Jawab :

Agar pernyataan tersebut bernilai true, maka ((A or not C) and (A and D or A and not D) or A and not C or not C) haruslah bernilai true dan (not E and (E or  not B) or (not B or E and E) and(E or B)) juga harus bernilai true.

((A or not C) and (A and D or A and not D) or A and not C or not C) → A = True, not C = True, D = False.

Uji : (T˅T)˄(T˄F˅T˄T)˅T˄T˅T) = (T˄T˅T˄T˅T) = True

(not E and (E or not B) or (not B or E and E) and(E or B)) → Not E = False, Not B = True

Uji : (F˄(T˅T)˅(T˅T˄T)˄(T˅F) = (F˄T˅T˄T) = (F˅T) = True

Jadi,

A = True, not C = True, D = False dan Not E = False, Not B = True

A = True, B = False, C = False, D = False, E =  True (B)

Read more...

Pembahasan KSN-K Informatika 2020 No. 15

Soal 15

Angga, Bandi dan Cinta diinterogasi oleh polisi atas pembunuhan dari Duduy. Bukti-bukti pada tempat

kejadian perkara (TKP) menunjukkan bahwa mungkin seorang pengacara terlibat pada perkara

pembunuhan. Mereka, salah satunya adalah pembunuh, membuat dua buah pernyataan sebagai

berikut.

· Angga memberi pernyataan:

o Saya bukan pengacara

o Saya tak terlibat pembunuhan Duduy

· Bandi memberi pernyataan

o Saya memang seorang pengacara

o Tetapi saya tak terlibat pembunuhan Duduy

· Cinta memberikan pernyataan

o Saya bukan pengacara

o Seorang pengacara yang membunuh Duduy

Pada pemeriksaan polisi ditemukan bahwa hanya dua dari pernyataan di atas yang benar dan ternyata

hanya satu dari ketiga orang itu yang bukan pengacara.

Siapakah yang membunuh Duduy?

a. Angga

b. Bandi

c. Cinta

d. Angga dan Bandi bersama-sama

e. Jawaban a, b, c, dan e salah.

Jawab :

Bukti-bukti pada tempat kejadian perkara (TKP) menunjukkan bahwa mungkin seorang pengacara terlibat pada perkara pembunuhan.

Pernyataan yang sudah benar adalah Bandi yang menyatakan bahwa dia memang seorang pengacara, tetapi dia tak terlibat pembunuhan Duduy.

Pada pemeriksaan polisi ditemukan bahwa hanya dua dari pernyataan di atas yang benar dan ternyata hanya satu dari ketiga orang itu yang bukan pengacara, maka ada 2 kemungkinan :

Kemungkinan 1

Jika Cinta yang berbohong (Pembunuh), maka pernyataan Cinta yang jujur menjadi : Saya pengacara dan bukan pengacara yang membunuh Duduy. Maka ini bertentangan dengan bukti pada tempat kejadian perkara (TKP) menunjukkan bahwa mungkin seorang pengacara terlibat pada perkara pembunuhan.

Kemungkinan 2

Jika Angga yang berbohong (Pembunuh), maka pernyataan Angga yang jujur menjadi : Saya pengacara dan saya terlibat dalam pembunuhan Duduy. Maka ini sesuai dengan informasi yang diberikan bahwa terdapat dua pernyataan yang benar, yaitu pernyataan Bandi dan Cinta, serta ada dua orang pengacara dan satu tidak pengacara. Maka pembunuh Duduy adalah Angga (A).

Read more...

Pembahasan KSN-K Informatika 2020 No. 13 dan 14

Soal 13

Tabungan Ambyar lebih banyak daripada jumlah tabungan Bela dan Kuya. Tabungan Bela lebih banyak daripada tabungan Kuya. Tabungan Denmas lebih banyak daripada jumlah tabungan Ambyar, Bela, dan Kuya. Pernyataan yang benar adalah?

a. Tabungan Ambyar lebih banyak daripada tabungan Denmas.

b. Jumlah tabungan Denmas dan Kuya sama dengan jumlah tabungan Ambyar dan Bela.

c. Tabungan Denmas merupakan penjumlahan tabungan Ambyar, Bela, dan Kuya.

d. Yang mempunyai tabungan paling banyak adalah Ambyar.

e. Kuya mempunyai tabungan paling sedikit.

Jawab :

Denmas >Ambyar> Bela > Kuya (E)

Soal 14 

Kwak adalah bebek yang paling tinggi di kandang Pak Dengklek. Kwik kalah tinggi dibanding Kwuk, tetapi Kwuk sama tingginya dengan Kwek.  Kwek lebih tinggi dari Kwok. Maka pernyataan yang benar berikut ini adalah...

a. Kwuk tidak lebih tinggi daripada Kwik.

b. Kwik tidak kalah tinggi daripada Kwak

c. Kwek lebih tinggi daripada Kwak

d. Kwek lebih tinggi daripada Kwik

e. Kwok lebih tinggi daripada Kwuk

Jawab :

● Kwak adalah bebek yang paling tinggi → Kwak > (Kwik, Kwuk, Kwek, Kwok)

● Kwik kalah tinggi dibanding Kwuk, tetapi Kwuk sama tingginya dengan Kwek →  Kwuk = Kwek > Kwik

● Kwek lebih tinggi dari Kwok → Kwek > Kwok

Tinjau semua option

a. Kwuk tidak lebih tinggi daripada Kwik (Bertentangan dengan pernyataan kedua)

b. Kwik tidak kalah tinggi daripada Kwak (Bertentangan dengan pernyataan pertama)

c. Kwek lebih tinggi daripada Kwak (Bertentangan dengan pernyataan pertama)

d. Kwek lebih tinggi daripada Kwik (Sesuai dengan pernyataan kedua)

e. Kwok lebih tinggi daripada Kwuk (Bertentangan dengan pernyataan ketiga)

Read more...

Pembahasan KSN-K Informatika 2020 No. 11 dan 12

Deskrispsi Untuk Soal Nomor 11 dan 12

Pak Dengklek menugaskan Kwak, Kwik, Kwuk, Kwek, dan Kwok untuk menjaga pekarangan berisi banyak bebek di belakang rumahnya. Setiap harinya biasanya terdiri 2-3 bebek yang harus menjaga dengan ketentuan sebagai berikut :

· Setiap bebek mendapat jatah tiga hari bertugas dan libur setiap Senin.

· Pada Selasa dan Jumat harus ada tiga bebek yang menjaga.

· Kwak bertugas selama tiga hari berturut-turut, termasuk Jumat.

· Kwek tidak bertugas di hari Minggu.

· Hari tugas Kwik dan Kwuk berselang-seling.

· Kwok selalu bertugas bersama Kwik.

11. Jika Kwuk bertugas pada Rabu, manakah pernyataan yang tepat?

a. Kwak bertugas dengan Kwok pada hari Selasa.

b. Kwuk bertugas pada hari Minggu dengan Kwek.

c. Kwok bertugas dengan Kwik dan Kwek pada Rabu.

d. Kwek bertugas dengan Kwuk dan Kwak pada Jumat.

e. Kwik bertugas bersama Kwak dan Kwok pada Kamis.

Jawab : Eliminasi pernyataan yang bertentangan dengan syarat yang diberikan

a. Kwak bertugas dengan Kwok pada hari Selasa. (Salah oleh syarat yang ketiga)

b. Kwuk bertugas pada hari Minggu dengan Kwek. (Salah oleh syarat yang keempat)

c. Kwok bertugas dengan Kwik dan Kwek pada Rabu. (Salah oleh syarat yang kedua)

d. Kwek bertugas dengan Kwuk dan Kwak pada Jumat.

e. Kwik bertugas bersama Kwak dan Kwok pada Kamis. (Salah oleh syarat yang kedua)

12.  Jika Kwuk bertugas pada Rabu, pada hari apa saja dipastikan yang jaga hanya ada dua bebek?

a.  Selasa, Rabu, dan Kamis

b. Rabu, Kamis, dan Minggu

c. Selasa, Kamis, dan Minggu

d. Rabu, Jumat, dan Sabtu

e. Jumat, Sabtu, dan Minggu

Jawab :

Selasa                Rabu                 Kamis              Jum’at               Sabtu             Minggu

     3                       2                         2                        3                        2                      2

Berarti, eliminasi pernyataan yang ada hari selasa dan jum’at. Pilihan yang tidak ada selasa dan jum’at hanya ada pada pilihan yang B

Read more...

Pembahasan KSN-K Informatika 2020 No. 9 dan 10

Deskripsi berikut digunakan untuk soal nomor 9 dan 10

Pada liburan kali ini, Pak Blangkon akan melakukan bersih-bersih pada 5 kandang ayamnya yakni kendang E, F, G, H, dan I. Karena kelima kandang tersebut saling berhubungan maka Pak Blangkon harus memperhatikan ketentuan berikut dalam menentukan urutan pembersihan kandang:

 Kandang H dapat dibersihkan jika kandang F sudah dibersihkan

 Kandang G harus dibersihkan sebelum membersihkan kandang E

 Kandang I dibersihkan pada urutan keempat 

9.  Urutan pembersihan kendang yang benar adalah …

    a.  I, G, E, F, H

    b. F, H, E, I, G

    c. H, E, G, I, F

    d. G, F, E, I, H

    e. G, I, F, E, H

10.  Jika Pak Blangkon membersihkan kandang G pada urutan kedua, maka pernyataan yang benar 

       adalah

       a. Kandang E dibersihkan pada urutan keempat 

       b. Kandang I dibersihkan pada urutan terakhir

       c. Kandang H dibersihkan pada urutan kelima 

       d. Kandang F dibersihkan pada urutan pertama

       e. Kandang E dibersihkan pada urutan pertama

Jawab : 

9.  Aturannya adalah 

 Kandang H dapat dibersihkan jika kandang F sudah dibersihkan

 Kandang G harus dibersihkan sebelum membersihkan kandang E

 Kandang I dibersihkan pada urutan keempat

Dari analisa yang sesuai dengan kondisi yang diberikan, berikut urutan kandang yang dibersihkan

  G    E     F      I     H

  1     2     3      4     5

  atau

  G    F    E      I     H    (D)

  1     2     3      4     5

10.  Jika Pak Blangkon membersihkan kandang G pada urutan kedua, maka :

  F     G    E      I     H

  1     2     3      4     5

d. Kandang F dibersihkan pada urutan pertama (D)

Read more...

Pembahasan KSN-K Informatika 2020 No. 8

Soal 8
Terdapat 100 permen. 91 diantaranya masih segar. Apabila permen tersebut akan dibagi rata ke dua
orang secara rata (masing-masing 50 permen, tetapi dibagikan secara acak), manakah fakta yang pasti
benar?
a. Terdapat satu orang yang memiliki permen segar >= 40
b. Terdapat dua orang yang memiliki permen segar >= 45
c. Terdapat satu orang yang memiliki permen segar >= 46
d. Terdapat satu orang yang memiliki permen segar >= 50
e. Pernyataan a, b, c, dan, d salah.
Jawab :
Terdapat 91 permen segar dan 9 permen tidak segar.
Kemungkinan 1
Orang pertama : 50 permen = 45 segar + 5 tidak segar
Orang kedua : 50 permen = 46 segar + 4 tidak segar

Kemungkinan 2
Orang pertama : 50 permen = 46 segar + 4 tidak segar
Orang kedua : 50 permen = 45 segar + 5 tidak segar

Kemungkinan Terburuk :
Orang pertama : 50 permen = 41 segar + 9 tidak segar
Orang kedua : 50 permen = 50 segar + 0 tidak segar

Dari segala kemingkina tersebut fakta yang pasti benar adalah Terdapat satu orang yang memiliki permen segar >= 46 (C). Karena pada kemungkinan terburuknya sudah jelas bahwa 50 > 46. Minimal terdapat 46 permen segar yang diperoleh oleh salah satu dari kedua orang tersebut.

Read more...

Pembahasan KSN-K Informatika 2020 No. 7

Pak Dengklek menjatuhkan sebuah bola pingpong dari ketinggian 25 m. Bola tersebut memantul kembali dengan ketinggian 4/5 kali tinggi semula. Pematulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah … m.
a. 200
b. 215
c. 225
d. 250
e. 235
Jawab :

Karena bola memantul terus-terusan sampai berhenti, berarti ini termasuk deret geometri tak hingga. Untuk mencari panjang lintasan bola yang memantul ini, rumus yang digunakan adalah

Panjang lintasan = ketinggian bola jatuh + 2(kali deret takhingga)

Dalam deret takhingga ini, yang menjadi suku pertamaya adalah pantulan pertama (bukan ketinggian bola jatuh pada awal).

Pantulan pertama a = 25 x 4/5 = 20 m (suku pertama)

Panjang Lintasan = 25 + 2(100) = 225 m

Read more...

Pembahasan KSN-K Informatika 2020 No. 6

Selvi naik taksi online berargo dari Kota P ke Kota Q yang berjarak 10 km. Besarnya argo taksi adalah Rp10.000,00 untuk 1 km pertama, kemudian bertambah Rp500,00 tiap 100 m selanjutnya. Besarnya ongkos taksi yang harus dibayar Selvi adalah?
a. Rp45.000,00
b. Rp54.500,00
c. Rp55.000,00
d. Rp65.500,00
e. Rp60.000,00

Jawab :
1 km pertama, biaya nya adalah Rp. 10.000,00
Tersisa 9 km lagi untuk mencapai tujuan. Dengan ketentuan, tiap 100 m bertambah Rp500,00
Hati hati jangan tertipu! Lihat polanya sebagai berikut
1000 m sudah bayar Rp. 10.000,00
1000 m    ↺   1100 m    ↺   1200 m    ↺   1300 m    ↺   1400 m ..... 10.000 m
              Rp500,00     Rp500,00        Rp500,00      Rp500,00      ....      Rp500,00 = 89 x Rp500,00
89 x Rp500,00 = 44.500
Jadi, total biaya yang dikeluarkan adalah Rp. 10.000,00 + Rp. 44.500,00 = 54.500,00 (B)

Read more...

Pembahasan KSN-K Informatika 2020 No. 5

Soal 5

Read more...

Pembahasan KSN-K Informatika 2020 No. 4

Soal 4
Sisa pembagian 1³+2³+3³+4³+...+100³ oleh 7 adalah...
a. 1
b. 2
c. 3
d. 4

e. 5

Jawab :
Kita tahu bahwa :

Maka, sisa pembagian 1³+2³+3³+4³+...+100³ oleh 7 adalah 2 (B)

Lanjut besok lagi ya. Bapak mau rehat dulu. hehe

Read more...

Pembahasan KSN-K Informatika 2020 No. 3

Soal 3
Dari kota A ke kota B dilayani oleh 4 bus dan dari B ke C oleh 3 bus. Seseorang berangkat dari kota A ke kota C melalui B kemudian kembali lagi ke A juga melalui B. Jika saat kembali dari C ke A, ia tidak mau menggunakan bus yang sama, maka banyak cara perjalanan orang tersebut adalah...
a. 12
b. 36
c. 72
d. 96
e. 144

Jawab :
Rute Pergi A > B > C = 4 x 3
Rute Pulang C > B > A = 2 x 3
Jadi, banyaknya rute perjalanan orang tersebut adalah  4x3x2x3 = 72 cara (C)

Read more...

Pembahasan KSN-K Informatika 2020 No. 2

Soal 2
Sebagai Pembina Olimpiade Komputer SMA Maju Bersama, Pak Dengklek menyiapkan 10 soal latihan, dari nomor 1 sampai nomor 10 yang harus dikerjakan oleh siswanya. Aturan pengerjaan soalnya adalah soal nomor 1, 3 dan 5 wajib dikerjakan tetapi para peserta hanya mengerjakan 8 dari 10 soal yang tersedia. Banyak cara peserta memilih soal yang dapat dikerjakan adalah?
a. 21
b. 28
c. 45
d. 48
e. 56

Jawab :
Aturan pengerjaan soalnya adalah soal nomor 1, 3 dan 5 wajib dikerjakan, berarti, tersisa 7 Soal yang tersedia. Akan tetapi, yang harus dijawab hanya sebanyak 8 soal. Sementara 1, 3 dan 5 wajib dikerjakan, maka 7 soal yang tersedia, dipilih 5 soal lagi untuk dikerjakan sehingga dapat ditentukan dengan aturan kombinasi berikut :
(7, 5) = 5!.6.7 = 3.7 = 21 cara (A)
             2!.5!

Read more...

Pembahasan KSN-K Informatika 2020 No. 1

Soal 1
Pak Dengklek memberikan tebak-tebakan kepada anaknya untuk menentukan nilai sebuah fungsi F(x, y) saat diberikan dua buah sembarang nilai x dan y. Jika diketahui bahwa F(3, 1) bernilai 24, kemudian F(5, 2) bernilai 37, dan F(7, 2) bernilai 59. Maka berapakah nilai F(7, 5) =…?
a. 211
b. 212
c. 222
d. 202
e. 242

Jawab :
Perhatikan polanya, sebuah barisan naik dengan ketentuan :
F(3, 1) = 24 = (3-1)x10 + (3+1) = 20+4 (Pengalinya adalah 10 karena hasil 3+1 masih 1 digit)
F(5, 2) = 37 = (5-2)x10 + (5+2) = 30+7 (Pengalinya adalah 10 karena hasil 5+2 masih 1 digit)
F(7, 2) = 59 = (7-2)x10 + (7+2) = 50+9 (Pengalinya adalah 10 karena hasil 7+2 masih 1 digit)

Dengan melihat pola tersebut, maka F(7, 5) dapat ditentukan sebagai berikut :
F(7, 5) = (7 - 5)x100 + (7+5) = 200 + 12 = 212 (B)
(Pengalinya adalah 100 karena hasil 7+5 adalah 2 digit, sehingga menjadi barisan naik)

Read more...

Latihan Elips

Latihan Elips. Download Here

Read more...